介入タイミングが複数あるときの差分の差分法：Staggered DiDの紹介

AI/機械学習

執筆者

公開日

2023.08.22

更新日

2024.05.16

当社のデータサイエンティストによるテックブログです。
今回は、DiD（差分の差分法）を取り上げます。DiDは、因果推論の書籍では必ずと言っていいほど紹介される古典的な手法でありつつ、学術的にここ数年で盛り上がっているトピックでもあります。
本ブログでは、新しく開発された手法の中からビジネスでデータ活用する上でも有用な手法について紹介します。

はじめに

こんにちは、データサイエンティストの田中です。先日土鍋で炊いたご飯が食べられるお店に行ったのですが、あまりの美味しさに土鍋の購入を検討しています。

本日は、差分の差分法（以下、DiD）の発展形についてご紹介します。DiDは因果推論の書籍では必ずと言っていいほど紹介される古典的な手法ですが、実は学術的にここ数年で盛り上がっているトピックでもあります。多くの新しい手法が開発されていますが、そのなかでもビジネスでデータ活用する上でも有用な手法について紹介します。

DiDとは何か

まずはDiDについて簡単に説明します。『効果検証入門』などに載っている内容なので、知っている人は次の節まで飛ばしても構いません。

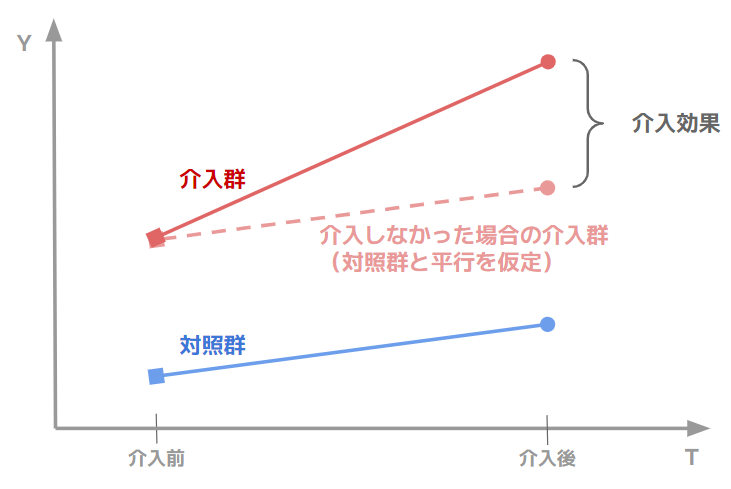
DiDとは介入群の介入前後の差分から、対照群の同時期の差分を引いたものを効果とみなす手法です（下図参照）。
これは「もし介入群に介入しなかった場合、差分は対照群と同じである」を仮定していることになります。本記事では、この仮定（いわゆる平行トレンドの仮定）が成り立つときを想定して話を進めます。

さて、実はDiDは回帰分析を用いて表現することができます。

ここで、

\(D_i\) : 介入群だと 1、対照群だと 0 をとるダミー変数
\(Post_t\) : 介入前だと 0、介入後だと 1 をとるダミー変数

です。従って \(D_i * Post_t\) の項は介入を受けたときだけ 1 をとる変数で、その回帰係数 \(\gamma\) が求めたい介入効果となります。このことを数式で確認しましょう。

こんなとき、どうする？

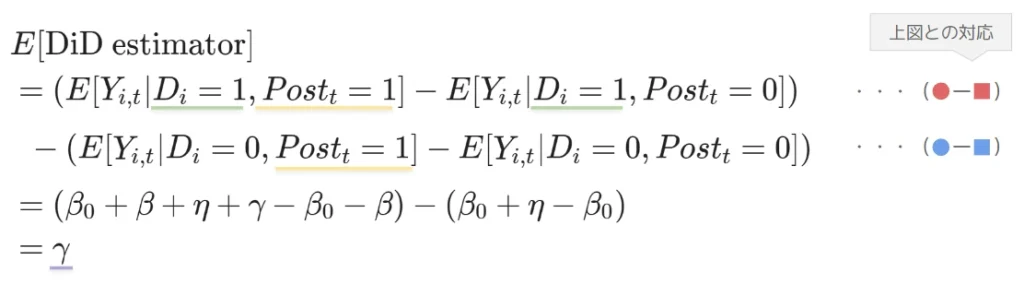
実際にDiDを使う際、以下のようなケースに直面することがあるかと思います。

① 動的な効果を知りたい
例）広告を見飽きて、効果が徐々に減退する

② 介入開始タイミングが複数ある
例）トライアル店舗で試したところ効果がありそうだったので、他の店舗もトライアルに追加した

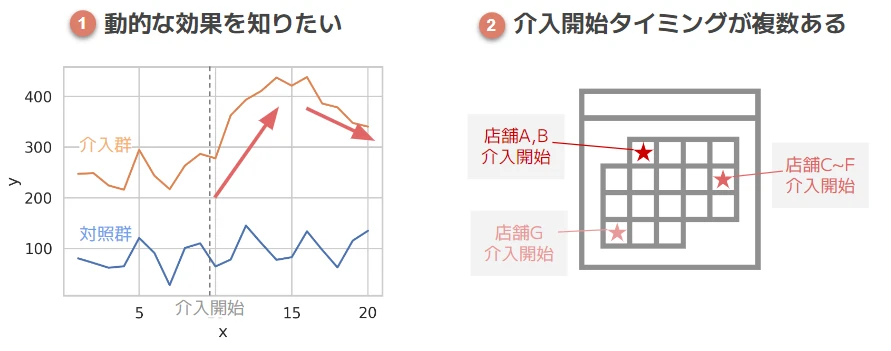
①に関しては、色々な長さの2期間での差分をとれば求められるかもしれません。②は対照群に関していつの差分をとるべきかを考える必要があります。また、基本のDiDだと2時点のデータしか使わないので、データを余すことなく使いたいというモチベーションもあります。

いずれにしろ、DiDに少し手を加えたものを使う必要がありそうです。これらを解決するような手法を紹介していきます。

拡張：Two Way Fixed Effect Event Study (TWFE Event Study)

上の回帰を以下のように拡張してみましょう。

パッと見は大きく異なりますが、以下3点のマイナーチェンジです。

介入群ダミー \(D_i\) → グループ固定効果 \(\beta_i\)
- 固定効果とは、グループごとに異なる切片を作ることを指します
- グループIDを OneHot Encoding したものを説明変数に加えることと同じです
介入後ダミー \(Post_t\) → 時間固定効果 \(\eta_t\)
- 多期間あるので、それぞれの期間について time dummy を入れるのに対応します
介入を受けたときだけ 1 をとる変数 → 介入を受け始めてから l 期のときだけ 1 をとる変数
- なお、l の範囲は -T から T までの間です（期間数を T とする。なお完全な多重共線性が生じないよう期間は適宜除く）

これで多期間を扱えるようになりました。\(\mathbf{\gamma_t}\) が介入開始から l 期経ったときの効果を表します。マイナス、つまり介入開始まで l 期のときの効果（平行トレンドの仮定が成り立つなら0になるはず）も含みます。
ちなみに、呼称としては単に Event Study と呼んだり、Dynamic DiD や Dynamic TWFE と呼ぶこともあるようです。

さて、この手法は②介入タイミングが複数あるときにも使えるでしょうか？
l はあくまでも介入開始からの相対的な期間なので、一見できそうです。

しかし、効果の大きさと介入タイミングに関連があるときにバイアスが生じることが知られています*1。これは平行トレンドの仮定が成り立ったとしても生じうるバイアスです。極端な場合、真逆の効果を算出してしまうこともあります。

これは、例えば店舗単位の施策だと以下のような場合が当てはまるでしょう。

効果が大きそうな店舗から順に導入を進めるケース
手を挙げてもらった店舗から順に導入するケース

１は自明ですが、２の場合も自身で効果がありそうだと思っている店舗から手を上げることが想定されるので、無視できません。

続いてこの問題に対する対処法を見ていきます。

拡張：Staggered DiD

効果の大きさと介入タイミングに相関があるときに生じるバイアスを除く方法として、Staggered DiD という手法が提案されています。

正確にはこの場面で使える手法がいくつも提案されており、それらの総称（およびこの問題設定そのもの）として Staggered DiD という言葉が使われている模様です。ちなみにStaggeredという単語はスタッガースタートという言葉で使われます。オールスター感謝祭のマラソンみたいにスタートをずらす方式で、ググるとラジコンレースとかでも使われる言葉みたいです。他では、時差出勤のことを staggered commuting と言ったり、物理の格子計算で微分を隣接点で定義せずに一個離れた点で定義するような手法にもStaggeredという呼称が使われるそうです。ということで、「Staggered」は段階を踏んで介入されていく様子を表しています。たぶん*2。

本記事ではそのなかでも比較的シンプルな Sun and Abraham (2021) の手法について説明していきます。

介入開始タイミングが同じグループのことをコーホートと呼びましょう。

TWFE Event Study だと「開始からの期数」ごとに効果を推定していましたが、「コーホート×開始からの期数」ごとに推定し、それを集約するのが Sun and Abraham (2021) の提唱する手法です。数式で書くとこんな感じになります。

あくまでイメージですが、こうすることで TWFE Event Study で悪さをしていた、介入開始時期が異なるコーホート同士の比較を適切に行えるようになります。

なお、\(\gamma_{c,l}\) を集約する際は、開始からの期間が l であるデータをもつコーホートのシェア（該当するグループのなかで、そのコーホートに含まれる確率）で重み付けした平均を使います。

説明としては以上です。意外とシンプルな手法ですが、どのような違いが出るのか、実際に使ってみましょう。

やってみた

完全なランダムデータだと面白くないので、実データに対してシミュレーションした効果の項を足した、半生成データで実験します。

データ・設定

アイオワ州の酒の販売データが公開されているので、その2019年のデータを County × 週で集計したものを使います*3。

設定としては、52週のうち13/25/37週目に介入される County が 25 ずつ、対照群の County が 23 あり、介入後は以下の分布に従って発生させた効果を足すようにします。

13週開始群：\(\mathcal{Normal}(80000, 10000)\)
25週開始群：\(\mathcal{Normal}(40000, 10000)\)
37週開始群：\(\mathcal{Normal}(10000, 10000)\)

こうしてできたデータが下図です。13週目(3月)、25週目(7月)、37週目(9月) あたりを境に増加している群があるのが分かると思います。

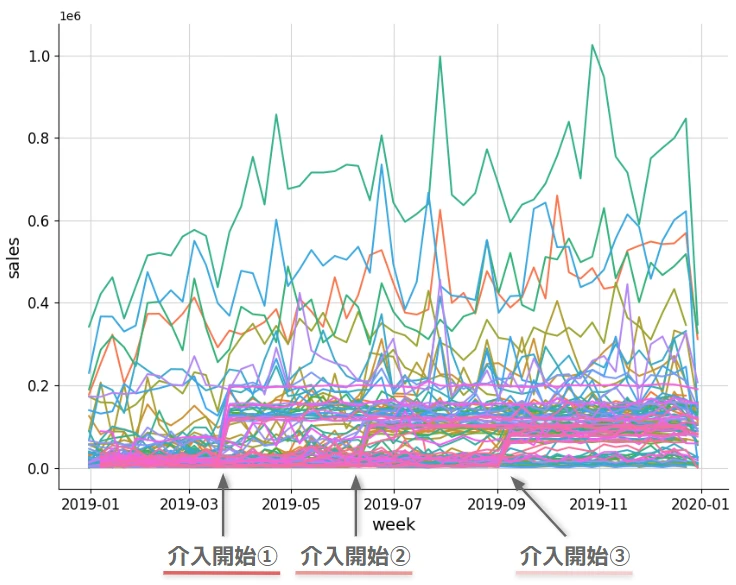
これを対象に TWFE Event Study、Staggered DID を推定していきます。

推定

R だと fixest というパッケージを用いて1行で推定できるのですが、python には私が知る限り存在しません。基本的には固定効果モデルの推定を応用するだけなので、今回は linearmodels というライブラリの、PanelOLS をベースにして書きました*4。

linearmodels を用いた TWFE Event Study

PanelOLS では、Pandas の Index に設定することで固定効果に相当する列を指定できます。

まず動的な効果を仮定しないシンプルな TWFE から作成していきます。ここではデータフレームの Index を固定効果として扱うことを宣言します。また、fit の際にクラスターのタイプを指定するようにします*5。

class Twfe(PanelOLS):
    def __init__(self, dependent, exog, **kwargs):
        # グループ・時間両方向に固定効果を入れて推定する
        super().__init__(dependent, exog, entity_effects=True, time_effects=True, **kwargs)

    def fit(self):
        # クラスターロバストな標準誤差を使用
        result = super().fit(cov_type='clustered', **{'cluster_entity': True, 'cluster_time': False})

        # 結果を格納
        self.coef_table = result.conf_int()
        self.coef_table['coef'] = result.params

        return result

続いて TWFE Event Study の場合を見ていきましょう（TwfeEsクラス）。この場合、\(\mathbb{I}[s_i – t = l]\) を作ってあげる必要があります。介入開始タイミングを持ったデータから説明変数exog、つまり介入開始からの期数ダミーを作成するメソッドを用意し、コンストラクタのなかで呼び出しています*6。それ以外は TWFE クラスと変わりません。

class TwfeEs(Twfe):
    def __init__(self, dependent, exog, start_col, **kwargs):
        """
        説明変数として「介入開始からの期数」列を作成
        
        Args:
            dependent (pd.Series): 被説明変数
            exog (pd.DataFrame): 説明変数
            start_col (str): exogのうち、介入開始タイミングが入ってる列の列名
        """
        exog = self._prepare_exog(exog, start_col)
        super().__init__(dependent, exog, **kwargs)

    def _prepare_exog(self, exog, start) -> pd.DataFrame:
        exog = exog.copy()
        time_col = exog.index.names[1]

        # 介入開始からの期数を作成し、One-Hot Encoding
        exog[time_col] = exog.index.get_level_values(time_col)
        exog['time_from_start'] = (exog[time_col] - exog[start]).astype('Int64')

        exog = pd.get_dummies(exog['time_from_start'], prefix='treated')

        # 完全な共線性を持つ変数を削除
        exog = exog.drop(columns='treated_-1')

        return exog

使用方法はこちらです。データに以下の処理を施して、上の自作クラスに突っ込みます。

対照群の介入開始時期を欠損にする
county、period を表す列を index に指定する
dependent を何への効果を知りたいか、exog を開始時期とする

import pandas as pd

df = pd.read_csv('./data/liquer_sales_datamart.csv')

# データの前処理
df['start_period'] = np.where(df.start_period==999, np.nan, df.start_period)
df = df.set_index(['county', 'period'], drop=False)
dependent = df.sales_treated
exog = df[['start_period']]

# TWFE Event Studyの推定
mod = TwfeEs(dependent, exog, 'start_period')
res_twfees = mod.fit()
print(res_twfees)

一応結果はこのような感じになります（以下で Staggered DiD と合わせてプロットしたものを見るので、詳細は割愛します）。

Included effects: Entity, Time
                           TwfeEs Estimation Summary
================================================================================
Dep. Variable:          sales_treated   R-squared:                        0.2192
Estimator:                     TwfeEs   R-squared (Between):              0.2202
No. Observations:                5033   R-squared (Within):               0.2970
Date:                Fri, Jun 16 2023   R-squared (Overall):              0.2232
Time:                        14:53:04   Log-likelihood                -5.833e+04
Cov. Estimator:             Clustered

（中略）

                              Parameter Estimates
===============================================================================
             Parameter  Std. Err.     T-stat    P-value    Lower CI    Upper CI
-------------------------------------------------------------------------------
treated_-36  2.861e+04  1.855e+04     1.5422     0.1231     -7758.7   6.497e+04
treated_-35   3.73e+04     7558.1     4.9354     0.0000   2.249e+04   5.212e+04
treated_-34   3.86e+04     8289.5     4.6567     0.0000   2.235e+04   5.485e+04

（中略）

treated_38   6.312e+04  1.167e+04     5.4101     0.0000   4.025e+04     8.6e+04
treated_39   7.149e+04  1.324e+04     5.4005     0.0000   4.554e+04   9.745e+04
treated_40   6.589e+04  1.637e+04     4.0246     0.0001    3.38e+04   9.799e+04
===============================================================================

F-test for Poolability: 448.75
P-value: 0.0000
Distribution: F(149,4807)

linearmodels を用いた Staggered DiD

基本的には TWFE Event Study の場合と変わりませんが、開始からの期数ダミーに変わって「コーホート×開始からの期数」ダミーを作成する処理を書きます。

class StaggeredDid(Twfe):
    def __init__(self, dependent, exog, start_col, **kwargs):
        """
        説明変数として「介入開始からの期数」列を作成

        Args:
            dependent (pd.Series): 被説明変数
            exog (pd.DataFrame): 説明変数
            start_col (str): exogのうち、介入開始タイミングが入ってる列の列名
        """
        exog = self._prepare_exog(exog, start_col)
        super().__init__(dependent, exog, **kwargs)

    def _prepare_exog(self, exog, start) -> pd.DataFrame:
        exog = exog.copy()
        time_col = exog.index.names[1]
        cohorts = list(exog[start].dropna().unique())

        # 介入開始からの期数×コーホートを作成し、One-Hot Encoding
        exog[time_col] = exog.index.get_level_values(time_col)
        exog['time_from_start'] = (exog[time_col] - exog[start]).astype('Int64')
        exog['time_from_start_x_cohort'] = exog.time_from_start.astype(pd.StringDtype()). 
            str.cat(exog[start].astype('Int64').astype(pd.StringDtype()), sep='_c')

        exog = pd.get_dummies(exog['time_from_start_x_cohort'], prefix='treated')

        # 完全な共線性を持つ変数を削除
        exog = exog.drop([f'treated_-1_c{int(i)}' for i in cohorts], axis=1)

        # 結果が見やすくなるように並び替え
        exog = exog[sorted(set(exog.columns), key=lambda x: int(re.search(r'_(.+)_', x).group(1)) )]

        return exog

    def aggregate_coef(self) -> pd.DataFrame:
        """結果を「開始からの期数」単位に集約する"""
        coef = self.coef_table
        coef = coef.reset_index(drop=False)
        coef['time_from_start'] = coef['index'].str.extract(r'_(.+)_').astype(int)
        coef['cohort'] = coef['index'].str.extract(r'c(.+)$').astype(int)

        # コーホート×開始からの期間ごとデータの数を重みとして使用する
        coef['cohort_size'] = coef.groupby(['cohort', 'time_from_start']).transform('size')

        # グループごとの加重平均を計算する関数
        def weighted_mean(group):
            return (group['coef'] * group['cohort_size']).sum() / group['cohort_size'].sum()

        weighted_means = coef.groupby('time_from_start', as_index=False).apply(weighted_mean)
        weighted_means.columns = ['time_from_start', 'coef']

        return weighted_means

こちらはこのような結果が得られます。

Included effects: Entity, Time
                            Sunab Estimation Summary
================================================================================
Dep. Variable:          sales_treated   R-squared:                        0.2813
Estimator:                      Sunab   R-squared (Between):              0.2410
No. Observations:                5033   R-squared (Within):               0.3715
Date:                Wed, Jun 21 2023   R-squared (Overall):              0.2480
Time:                        00:17:59   Log-likelihood                -5.812e+04
Cov. Estimator:             Clustered

（中略）

                                Parameter Estimates
===================================================================================
                 Parameter  Std. Err.     T-stat    P-value    Lower CI    Upper CI
-----------------------------------------------------------------------------------
treated_-36_c37    -1927.1  1.645e+04    -0.1172     0.9067  -3.417e+04   3.032e+04
treated_-35_c37     6685.9     8710.1     0.7676     0.4428  -1.039e+04   2.376e+04
treated_-34_c37     4818.6     7206.5     0.6687     0.5038     -9309.4   1.895e+04

（中略）

treated_38_c13   8.291e+04  1.664e+04     4.9832     0.0000   5.029e+04   1.155e+05
treated_39_c13   8.432e+04  1.955e+04     4.3135     0.0000     4.6e+04   1.226e+05
treated_40_c13   9.437e+04  1.946e+04     4.8492     0.0000   5.622e+04   1.325e+05
===================================================================================

結果

推定結果を見ていきましょう。下図に、TWFE Event Study、Staggered DiD の推定値を示しています。横軸が開始からの期数、先ほどの表現だと l にあたるものです。マイナスは開始より前を表します。縦軸は係数（介入効果, \(\eta\)）です。Staggered DiD は aggregate_coef メソッドを使って各コーホートの推定結果を集約した数字をプロットしています。

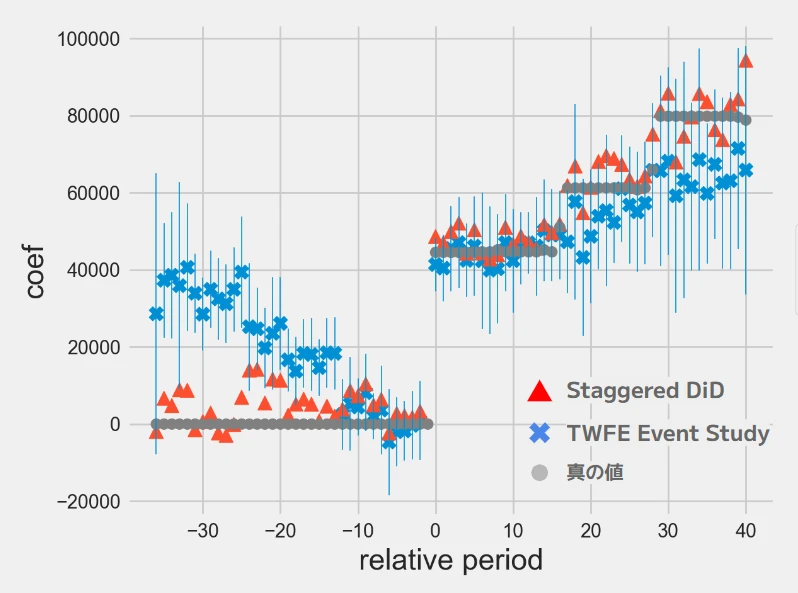
赤△が Staggered DiD、青✕が TWFE Event Study、灰〇が真の値です。一応 R の fixest パッケージで求めたものと一致することは確認しています（Staggered DiD の信頼区間は少しだけ面倒だったので計算していません…）。

TWFE Event Study（青✕）は、（１）介入前の効果が正に出てしまっている、（２）（30週以降特に）過少に推定される傾向にある、という結果となりました。

一方で Staggered DiD（赤△）は概ね真の値に近い数字となっています。例えば開始から30週（x軸が30）のあたりは13週目に介入開始したコーホートしかデータにないので、その平均の80,000ほどになります。

おわりに

今回は結果が分かりやすいよう極端な数字でシミュレーションしましたが、実データに適用する場合もある程度の差異が出てしまうケースはあるでしょう。介入タイミングと効果の大きさに関連がある場合、 Staggered DiD のような手法を用いる必要性が分かりました（逆に関連がない場合、TWFE Event Study も十分使えます）。

CausalImpact も似た目的で使えますが、あちらは基本的に単一系列に関する手法なので、複数系列のデータがあり今回紹介した手法が有用なケースも多いと思います。また、今回は処理内容を追えるよう python で実装しましたが、実際は無難に R のライブラリを用いるのがいいでしょう。

ということで、縄文時代の土器にルーツを持つ土鍋と同じく、170年以上前の John Snow の時代から長く愛されている差分の差分法の、最近の進展についてでした。このトピックはまだまだ技術的な発展がありそうなので、今後も注目していきたいと思います。

ブレインパッドでは新卒採用・中途採用共に一緒に働く仲間を募集しています。
ご興味のある方は、ぜひ採用サイトをご覧ください！

株式会社ブレインパッド｜新卒・中途採用

参考

https://www.sciencedirect.com/science/article/abs/pii/S030440762030378X
- Sun, L., & Abraham, S. (2021). Estimating dynamic treatment effects in event studies with heterogeneous treatment effects. Journal of Econometrics, 225(2), 175-199.
https://www.sciencedirect.com/science/article/abs/pii/S0304407621001445
- Goodman-Bacon, A. (2021). Difference-in-differences with variation in treatment timing. Journal of Econometrics, 225(2), 254-277.
https://cran.r-project.org/web/packages/fixest/vignettes/fixest_walkthrough.html
- R の fixest パッケージの vignettes
- 「4.2.2 Simple difference-in-differences (TWFE) 」に TWFE Event Study、「4.2.3 Staggered difference-in-differences (Sun and Abraham, 2020) 」に Staggered DiD について記載がある
https://bashtage.github.io/linearmodels/panel/panel/linearmodels.panel.model.PanelOLS.fit.html#linearmodels.panel.model.PanelOLS.fit
- linearmodels のドキュメント
https://github.com/kazuyanagimoto/staggered_did_tutorial
- 慶応の小西先生による日本語チュートリアル「DIDの計量経済手法の近年の展開」のサイト
- Stat, R のコードあり
https://matheusfacure.github.io/python-causality-handbook/24-The-Diff-in-Diff-Saga.html
- 24 – The Difference-in-Differences Saga — Causal Inference for the Brave and True
- 2. Death: Failures over Effect Heterogeneity の treatment-effect-heterogeneity-in-time の節が、コーホート同士の不適切な比較が起こる例を直感的に説明している
- 本記事と同じく Sun and Abraham (2021) を、こちらは python の statsmodels を使って書いてる
https://mixtape.scunning.com/09-difference_in_differences
- Causal Inference The Mixtape – 9 Difference-in-Differences
- 最近和訳も出た mixtape だが、冒頭の John Snow の話をはじめ、応用例が多く分かりやすい
- 9.6節が今回の話に対応する
https://diff.healthpolicydatascience.org/
- Difference-in-Differences
- 仮定や条件付きのケースが丁寧に整理されている。パラメータなどを動かしながら振る舞いを理解できるようなページになっている

*1: 特に、介入群がない場合におかしな結果になりやすいです。このバイアスの有無は Goodman-Bacon (2021) で提案されている診断手法 (Rのライブラリは bacondecomp) などで診断できます。
バイアスが起こる原因について、Sun and Abraham (2021) は「the coefficient on a given lead or lag can be contaminated by effects from other periods」と述べています。また、 24 – The Difference-in-Differences Saga — Causal Inference for the Brave and True は他期間の介入が原因でコーホート同士の比較が上手くいかない例を直感的に説明しています。

*2:ちなみに私は長いことステージ (Stage) と同根だと勘違いしていましたが、よろめくを意味する stakeren あたりが由来で全然違うみたいです。恥ずかしい。

*3:https://data.iowa.gov/Sales-Distribution/2019-Iowa-Liquor-Sales/38×4-vs5h. なお、County は日本の市区町村よりひとつ大きい単位の行政区分です（厳密に対応している訳ではないので大雑把な説明ですが）。あえて日本語にすると「郡」ですが、群と紛らわしいので英語で書いています。

*4:linearmodels.panel.model.PanelOLS – linearmodels 5.4

*5:DiDの設定だと回帰の仮定（誤差項は互いに独立）を逸脱するため、cluster robust な標準誤差を用いて調整する必要があります。こちらで紹介されてるイラストが分かりやすいです。今回は county のほうだけクラスターに指定します。

*6:完全な多重共線性を避けるため、適宜変数を削除しています

このページをシェアする

コピー
しました

この記事に関する
お問い合わせはこちら

あなたにオススメの記事

人気タグから探す

人気記事ランキング

あなたにおすすめの記事

株式会社ブレインパッドについて

2004年の創業以来、「データ活用の促進を通じて持続可能な未来をつくる」をミッションに掲げ、データの可能性をまっすぐに信じてきたブレインパッドは、データ活用を核としたDX実践経験により、あらゆる社会課題や業界、企業の課題解決に貢献してきました。そのため、「DXの核心はデータ活用」にあり、日々蓄積されるデータをうまく活用し、データドリブン経営に舵を切ることであると私達は考えています。

株式会社ブレインパッド
についてはこちら

メールマガジン

Mail Magazine

データ活用の厳選記事や、会員限定のDXのお得情報などをお届けいたします。

1分で簡単登録！

メールマガジンのご案内