拡散モデルのデータサイエンスへの応用事例

はじめに

拡散モデルは、大規模言語モデルと並んで生成AIを支える基盤技術のひとつです。大規模言語モデルが、文章などの系列データの生成を得意とするのに対して、拡散モデルは画像、音声、動画など多様なデータを生成することができます。Sora2など、最近の動画生成における著しい性能改善の背後には、大規模言語モデルによる現実世界を反映したプロンプト理解と、拡散モデルによるプロンプト内容を忠実に再現する動画生成技術の発展があります。

データ生成における拡散モデルの汎用性は、画像や動画などのコンテンツにとどまりません。多様なデータを分析して将来予測や意思決定に役立てるデータサイエンスにおいても、拡散モデルを活用できる機会は多分にあります。本稿では、データサイエンスにおける拡散モデルの活用事例をいくつか紹介します。

拡散モデルとは

具体的な活用事例を紹介する前に、そもそも拡散モデルとは何なのかを解説します。

拡散モデルは、正式にはデノイジング拡散確率モデル（Denoising Diffusion Probabilistic Model; DDPM）^※1と呼ばれます。ここでいう「拡散」とは、画像や音声などの元データにノイズを段階的に加えて破壊していく過程を意味しています（図1）。例えるなら、ガラス板の上に砂で描かれた絵に、振動（ノイズ）を徐々に加えて砂絵が拡散して消えて行く様子に似ています。デノイジングとは、この拡散過程を逆向きにたどって段階的にノイズを除去する（denoise）ことで、元データを復元することを意味しています。拡散過程も、その逆向きの生成過程も、ともに確率分布によるサンプリングの連鎖なので確率モデルとして記述されます。拡散過程はノイズを付与するだけですが、生成過程ではノイズ除去をニューラルネットワークで学習することになります。

^{※1 参考文献：J. Ho et al., Denoising Diffusion Probabilistic Models. In Proc. NeurIPS, 2020; arXiv:2006.11239}

画像生成などのデータ生成モデルとしては、拡散モデルの他に敵対的生成ネットワーク（GAN）^※2や変分オートエンコーダ（VAE）^※3が知られています。どちらもニューラルネットワークで実装されますが、それぞれ課題を抱えています。GANは、特定のサンプルだけを生成するというモード崩壊が起こりやすく、学習が不安定になるという課題があります。一方、VAEは、学習は安定していますが、生成される画像の品質に限界があります。

関連記事：ビジネスを取り巻くAI・DXの現状と未来～第7回 生成AIの概要と適用例

^{※2：参考文献：I. J. Goodfellow et al., Generative Adversarial Networks. In Proc. NeurIPS, 2014; arXiv:1406.2661
（補足）GAN (Generative Adversarial Network) では、ノイズから画像データを生成する生成器と、生成された画像データが本物の画像か生成物かを見分ける識別器とを競わせながら敵対的に学習します。そのため、識別器の判定をすり抜ける特定のサンプルだけを生成するように学習が進んでしまうモード崩壊と呼ばれる現象が発生します。}

^{※3 参考文献： D. P. Kingma and M. Welling, Auto-Encoding Variational Bayes. In Proc. ICLR, 2014; arXiv:1312.6114
（補足）VAE (Variational Auto-Encoder) は、画像データを低次元の確率分布に圧縮するエンコーダ（符号器）と、その確率分布からサンプリングされた情報をもとに画像データを復元する復号器（デコーダ）とから構成されます。VAEの学習後は、デコーダのみを使って画像データを生成します。}

拡散モデルは、VAEと同様に学習が安定していて、GANを上回る高品質な画像データを生成できます。また、所与の条件（例えば、花の色や形など）を満たす画像データのみを生成するモデルを学習することも可能です（条件付き生成モデル）。さらに、画像データとその説明文の対応関係を学習したCLIPと組み合わせることで、文章（プロンプト）で指示したとおりの画像や動画を生成するモデルを実現することもできます。DALL·E 2、Stable Diffusionなどの画像生成サービス、Sora2などの動画生成サービスも、そのデータ生成の基本原理は拡散モデルによる条件付き生成です。

以下、拡散モデルのデータサイエンスへの応用について解説します。データサイエンスで重要となるのは、データ分析のもととなる表形式データです。本稿では、具体例としてふたつ、表形式データを生成する手法（TABSYN）、治験データから因果効果を推論する手法（DiffPO）を紹介します。

表形式データの生成

一般にデータ生成においては、元データの共通の特徴を満たしながらも、元データには存在しない新たなデータを生成することが期待されます。例えば、人物の顔画像を多数学習した生成モデルは、元データに存在しない多種多様な人物の顔画像を生成します。もし、元データに含まれている画像と同じ画像を生成するなら単純なコピーと変わりません。また、元画像のコピーでなくても、元画像の人物を特定できる画像を生成すれば、著作権や肖像権に抵触します。

表形式データにおいても同じ課題が生じます。例えば、電子カルテのデータは個人の既往症などの個人情報を含みます。表形式データを生成する場合、各列の分布や列間の相関係数といった統計的性質は元データと同じでも、ひとつとして元データと同じレコード行が存在しない表形式データを生成することが期待されます。

以下にそのような手法として、拡散モデルを使って表形式データを生成するTABSYN^※4を紹介します。

^{※4 参考文献：H. Zhang et al., Mixed-Type Tabular Data Synthesis with Score-based Diffusion in Latent Space. In Proc. ICLR, 2024; arXiv:2310.09656}

手法の解説

表形式データとは、学生の成績表のように数値やラベルが行と列に並んだ「表」として表されるデータのことです。表の各「列」はデータに共通した属性を表す変数（特徴量）であり、表の各「行」は変数に具体的な値が記入された記録（レコード）に対応します。成績表の例で見てみましょう。列には、生徒の属性（性別、誕生月など）、生徒の各科目の点数が並びます。行には、各生徒の属性と成績が記録されます。ちなみに、性別、誕生月のように複数のラベル（選択肢）からなる変数をカテゴリ変数、各科目の点数のように連続する数値で表される変数を数値変数と呼びます。

TABSYNでは、表形式データの列ごとの数値やラベルの頻度分布、列間の相関関係を既存の表形式データから学習します。学習したモデルを使ってサンプリングすることで、学習した表形式データと同じ統計的性質を持つデータレコードを生成します。ただし、表形式データの列には数値変数やカテゴリ変数が混在するので、拡散モデルを適用するには、以下に述べる工夫が必要となります。

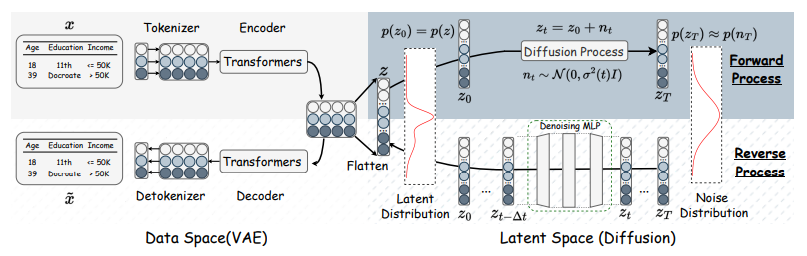
文書データを扱う自然言語処理では、文章は単語に分解され、単語は固定次元に埋め込まれた数値ベクトルとして表されます（Word2Vec）。表形式データの「行」を文章と見なせば、「列」に対応する数値やラベルは単語とみなすことができます（図2の\(x\)）。そこで、Word2Vecを適用して数値やラベルを固定次元のベクトルに埋め込みます（図2のトークナイザ）。

文章に含まれる単語間の関係性は、エンコーダと呼ばれるニューラルネットに通すことで符号化されます。最新の言語モデルでは、エンコーダとしてTransformerを採用することにより、単語間の関係性や文脈を自己注意機構（Self-Attention Mechanism）によって学習します（図2のEncoder）。TABSYNもエンコーダとしてTransformerを採用しています。表形式データの各行は、トークナイザとエンコーダを通って固定次元のベクトルを列数だけ並べた特徴量ベクトル\(z\)に変換されます。この\(z\)の分布を拡散モデルで学習することで、任意のガウスノイズから特徴量\(z\)を生成できるようになります（図2のForward Process：前向き過程、Reverse Process：逆向き過程）。

学習済みの拡散モデルからサンプリングされた\(z\)をTransformerによるデコーダで復号し、さらにトークナイザと同じWord2Vecでデータレコードに変換することで元の表形式データの特徴を反映したデータレコードを好きなだけ生成できます（図2の\(x̃\)）。

手法の評価

TABSYNの評価は、この手法で生成された表形式データの品質により評価されます。品質評価の観点として以下の3つが考えられます。

1. 生成データが元データの統計的性質を忠実に再現できているか。
2. 生成データが元データに含まれるレコードと類似したレコードを含んでいないか。
3. 生成データを使って学習した機械学習モデルの性能が、元データで学習した場合と比べて劣化していないか。

第1と第2の観点では、TABSYNによる表形式データの再現性を評価しています。参考までに他の生成モデルにおける結果とも比較します。一方、第3の観点では、TABSYNによる生成データの実用性を他の生成モデルと比較して評価しています。

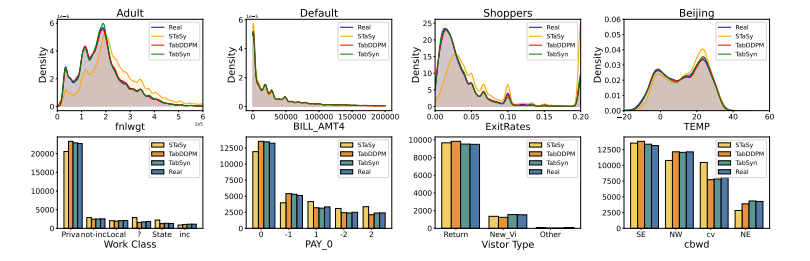
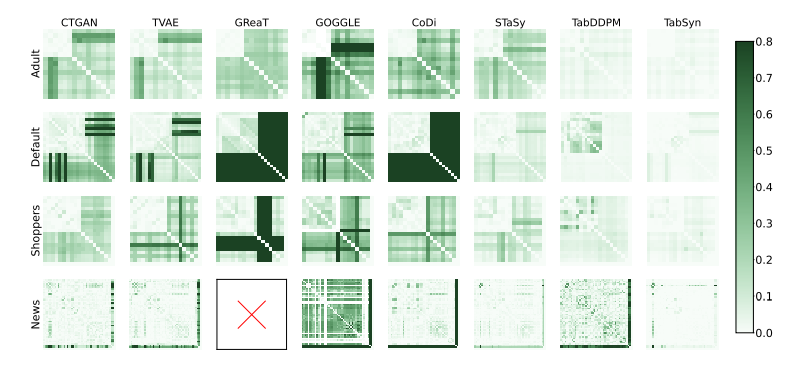
第1の観点では、生成データの列ごとのヒストグラム（1変数の分布）および、列間の関係性（2変数の相関係数）を元データと比べます。6種類のデータで検証した結果、生成データは変数ごとの分布形状、変数間の相関係数ともに、元データと類似の結果を再現することが分かりました（図3、図4）。論文では、図による定性的な評価だけでなく、統計量を用いた定量的な比較も行っています（付録の表2, 表3を参照）。

論文では扱われていませんが、1変数分布の類似性を理解するのによく使われる方法としてQ-Qプロットが知られています。Q-Qプロットは、2つの分布A、Bの同じ分位点について、分布Aの変数値を横軸、分布Bの変数値を縦軸としてプロットした図です。分布Aと分布Bの形状が等しければ、Q-Qプロットの散布図は、原点を通る対角線上に並ぶはずです。

試しに、6種類のデータのうちAdultデータの幾つかの変数でQ-Qプロットを見てみました。図5がその結果です。横軸は元データ、縦軸はTABSYNによる生成データの値です。図より、散布図は概ね対角線上に並んでおり、TABSYNが元データを正確に再現していることが分かります。

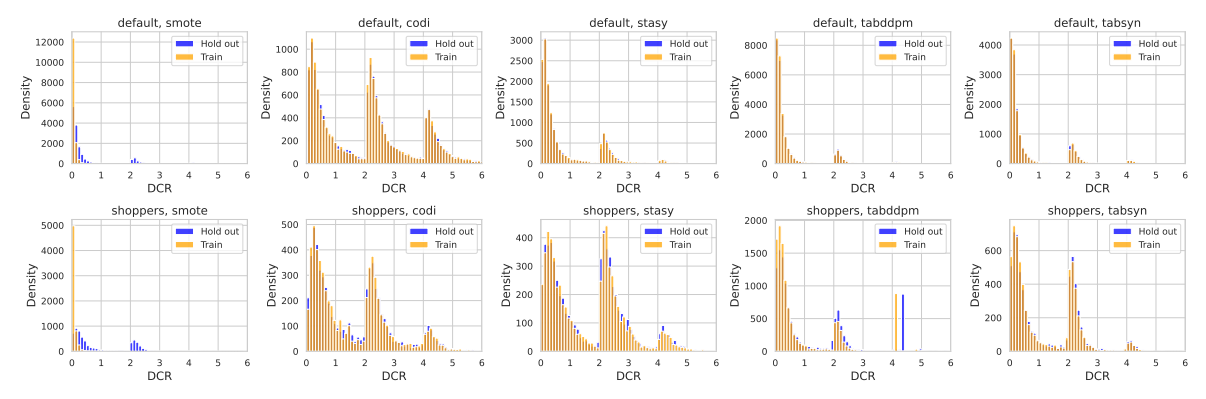
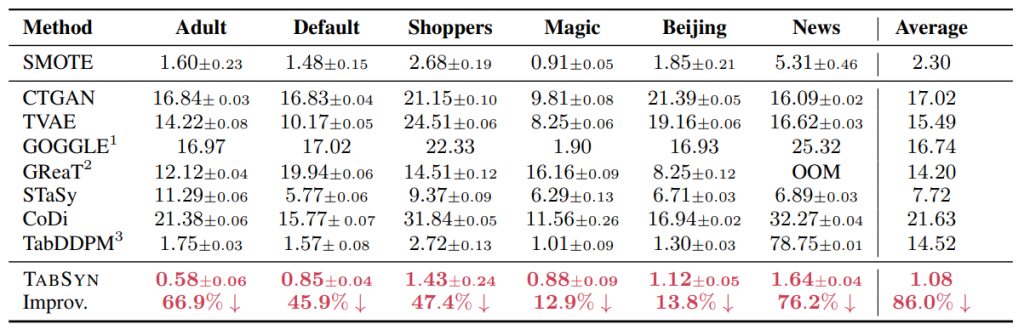
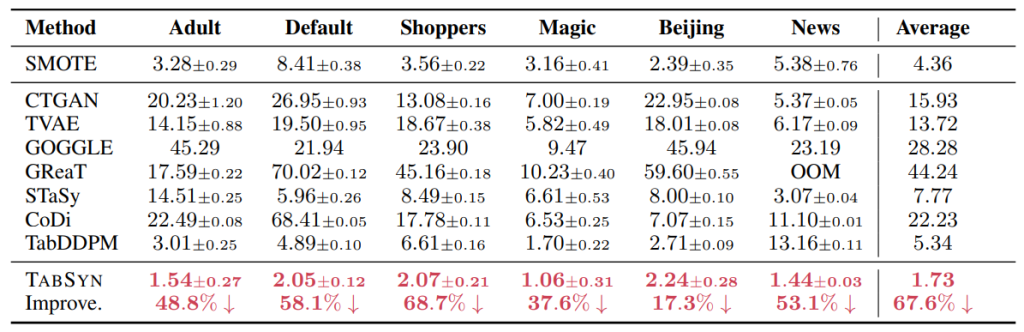
第2の観点では、生成データが元データに含まれるレコード行と同じか類似したレコードを含まないことを確認します。具体的には、生成データの各レコード行に対して、元データのレコード行との距離の最小値（DCRスコア^※5）を計算します。比較のため訓練データと同じ行数の元データをテストデータとして取っておき、生成データとテストデータのDCRスコアも計算します。もし生成データが訓練データと同様のデータを含んでいれば、訓練データで計算したDCRスコアの分布はゼロ近傍に集中し、テストデータで計算したDCRスコアはゼロから離れた位置に分布するので、両者の分布に違いが生じるはずです（図6）。DCRスコアの分布を訓練データとテストデータで比較してみると、元データに対する内挿とノイズ付与による生成データ（SMOTE）では、両者の分布に上述の差が表れますが（図6 左端）、TABSYNによる生成データでは両者の分布は概ね一致しており（図6 右端）、生成データが元データに類似のデータを含んでいないことが分かります。

^{※5 参考文献：F. M. Trudslev et al., A Review of Privacy Metrics for Privacy-Preserving Synthetic Data Generation. arXiv:2507.11324
（補足）DCRは、Distance to Closest Record の略称です。}

第3の観点では、訓練データと生成データのそれぞれで学習したモデルの性能を、共通のテストデータにおいて比較します。具体的には以下の手順に従います。

1. 元データを訓練データとテストデータに分割する。
2. 訓練データで学習したTABSYNを使って、訓練データと同じ行数のデータを生成する（生成データ）。
3. 生成データで訓練・チューニングした機械学習モデル(A)と、訓練データで訓練・チューニングした機械学習モデル(B)を、それぞれ共通のテストデータに適用して予測性能を比較する。

生成データが高品質であれば、モデル(A)の予測性能はモデル(B)に及ばないものの劣化の度合いは小さいはずです。6種類のデータでTABSYNを他の生成モデルと比較した結果、生成データによる性能劣化はTABSYNが他のモデルに比べて有意に小さい結果となっています（表1の最下行にあるTABSYNがモデル(A)、最上行にあるRealがモデル(B)の結果）。

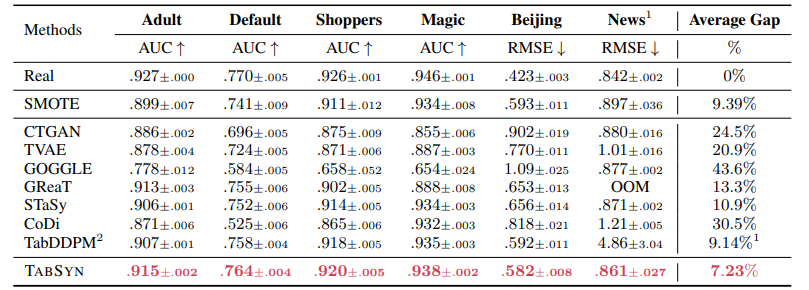
以上、3つの観点でTABSYNを評価してきました。比較対象には、GANおよびVAEを表形式データ生成に適用した手法（CTGAN、TVAE）の他、拡散モデルを適用したTabDDPMも含まれていますが、総じてTABSYNによる生成データの品質が高いと言えます。

因果推論への応用

2番目の事例として、因果推論への応用事例をとりあげます。ここでは、複数の患者の治験データから薬や治療法の処置効果を推定する例を考えます。

因果推論では、複数の患者の治験データから薬や治療法の処置効果を推定します。処置効果を見るには、病状のある患者に対して、薬を飲んだ場合（処置あり）と薬を飲まなかった場合（処置なし）とで、病状の回復に差があるか観測する必要があります。

ところが、一人の患者に対して、処置ありと処置なしの両方の結果を観測することはできません。例えば、薬を飲んで回復した患者を、再び病気にして今度は薬を飲ませないという治験は、倫理上問題があるため実施できません。仮に実施できたとしても、1回目の知見で薬を飲んだことの影響を排除することができません。このように、「同じ患者において、処置ありの結果と処置なしの結果を同時に観測できない」という問題は、因果推論の根本問題として知られています。

ある患者が処置を受けた場合、観測された「処置あり／なし」の結果に対して、観測されない「処置なし／あり」の結果を潜在的結果（Potential Outcome）と呼びます。潜在的結果を想定することは、現実には起こらなかったことを想定するので反実仮想と呼ばれます。通常の因果推論では、複数の患者を処置ありグループ（処置群）と処置なしグループ（対照群）とに分けて、グループごとに患者の属性（共変量）から観測結果を予測する機械学習モデルを学習します。同じ共変量に対してモデルの予測値の差から処置効果を推定できます。

拡散モデルを因果推論に適用する場合、処置のあり／なしを処置変数\(A＝1\)または\(0\)として、共変量とともに患者属性を表す条件として扱います。その条件のもとで観測結果と潜在的結果の両方をひとつの条件付き確率分布として学習します。以下では、上述のシナリオによる拡散モデルの適用例としてDiffPO^※6を紹介します。

^{※6 参考文献：Y. Ma et al., DiffPO: A causal diffusion model for learning distributions of potential outcomes. In Proc. NeurIPS, 2024; arXiv:2410.08924}

手法の解説

DiffPOの仕組みは、以下の図7に集約されています。

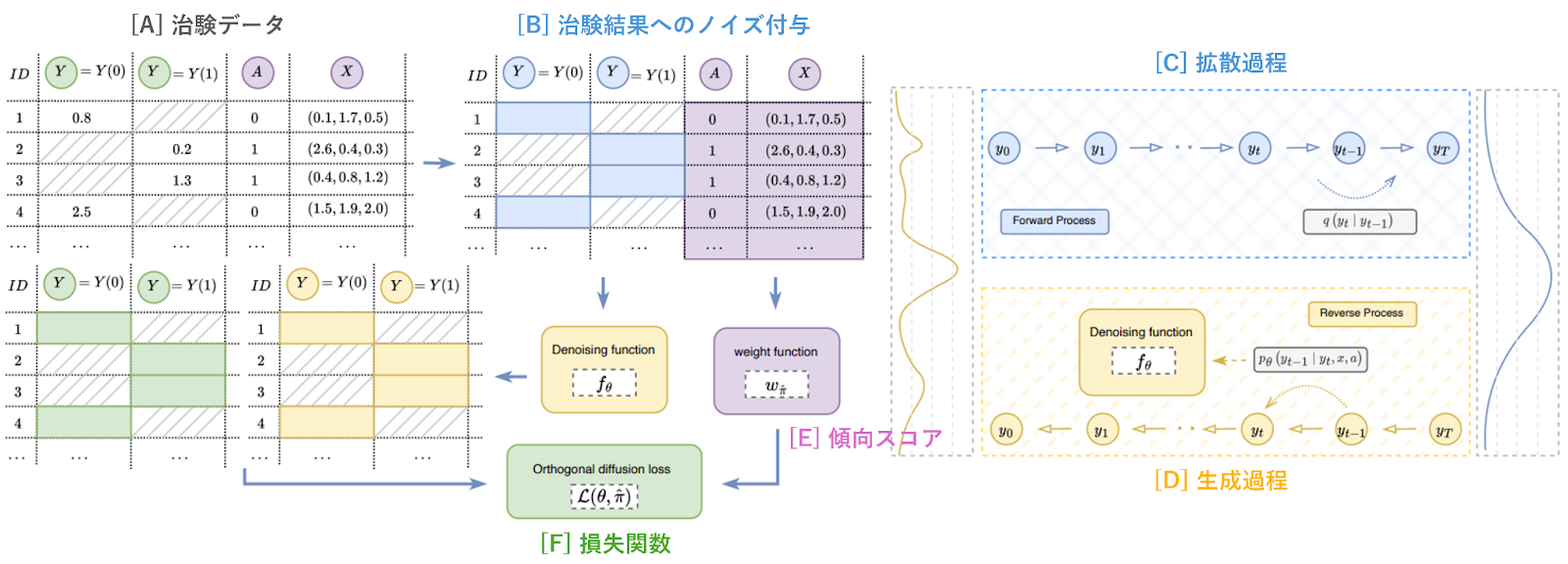
図7の左上にある表形式データ[A]は、複数の患者の治験データです。緑色の2列は、左から処置なしの結果\(Y=Y(0)\)と処置ありの結果\(Y=Y(1)\)が記録されています。各行は一人の患者に対応しており、処置ありか処置なしのうち観測された結果が記録されており、反実仮想の結果は欠損となっています。

表形式データの紫色の2列は、左から処置変数\(A\)と共変量\(X\)が記録されています。処置なしの患者は\(A=0\)、処置ありの患者は\(A=1\)が割り当てられており、\(A\)の値に対応した結果が観測値として緑色のY列に記録されています。図7の中央上の表形式データ[B]では、観測結果Yが青色の拡散過程（図7 右上[C]）に対応付けられています。観測結果\(Y\)の分布は、拡散過程の段階的なノイズ付与を経て、当初の非自明な分布から図7の右端にある自明なガウス分布にまで破壊されます。

ガウス分布からサンプリングされたデータは、黄色で示される逆向き過程の段階的なノイズ除去を経て観測結果Yを生成します（図7 右下[D]）。ニューラルネットによるノイズ除去の学習は、損失関数（図7 中央下[F]）の最小化問題に帰着します。損失関数の計算において、処置変数と共変量から学習された傾向スコアを使ってバイアス補正することにより（図7 中央下[E]）、処置群と対照群の共変量分布の違いを考慮した潜在的結果の分布推定を行うことができます。

DiffPOの論文では、ノイズ除去を学習するニューラルネットワークとして、時系列データの欠損補完を行う拡散モデル手法であるCSDI^※7のアーキテクチャを採用しています。CSDIでは観測データの一部を生成すべき欠損値と見なし、それら生成対象データの分布を残りの観測データを条件とする条件付き確率分布として学習します。このとき拡散モデルのノイズ付与の対象となるのは生成対象データのみです。因果推論の場合、治験の観測結果を生成対象データ、処置変数と共変量を条件付け用データと見なせば、CSDIのフレームワークがそのまま適用できます。

^{※7 参考文献：Y. Tashiro et al., CSDI: Conditional Score-based Diffusion Models for Probabilistic Time Series Imputation. In Proc. NeurIPS, 2021; arXiv:2107.03502}

以上をまとめると、DiffPOでは、処置変数と共変量で条件付けされた観測結果の分布\(p(Y|A,X)\)を学習します。分布関数の引数\(A,X\)として反実仮想の組合せも含んでいるので、結果的に\(p(Y|A,X)\)は観測結果と潜在的結果の分布を区別することなく表しています。

【補足】拡散モデルが条件付き分布\(p(Y|A,X)\)を学習するとは、具体的にどういうことかを説明します。拡散モデルでは、データに加えたノイズを少しずつ取り除いていく「逆拡散過程」をニューラルネットワークで学習します。各ステップでは、ニューラルネットワークがガウス分布に基づいてノイズを除去し、新しいサンプルを生成します。このノイズ除去のステップを順に繰り返して最終的に得られるサンプルは、結果として条件付き分布\(p(Y|A,X)\)から生成されたサンプルと同等である、ということです。

人工データの作成

因果推論では、共変量\(X\)で条件付けされた平均処置効果（Conditional Average Treatment Effectの頭文字をとってCATEと呼びます）を算出します。モデルの予測精度を見るには正解データとして反実仮想も含めた人工データを用意する必要があります。今回の検証では、論文に倣って、共変量はACIC2018の公開データから取得し、それをもとに以下の数式に従って処置変数\(A\)および結果\(Y(0),Y(1)\)を作成しました。人工データの内訳は、被験者数10,000人のうち処置群が4,328人、対照群が5,672人となっています。ここで、処置群と対照群とで共変量分布に差が出るように傾向スコアを使って調整してあります。

手法の評価

DiffPOの論文では、比較対象のモデルとしてニューラルネットワークにより実装された機械学習モデルを採用しています。しかし、データ分析の現場では、計算コストが低くて高精度な結果が期待できるツリー系アンサンブルのモデルが一般的に使用されます。ここでは、ランダムフォレストにより実装された機械学習モデルを比較対象とします。

因果推論において、共変量\(X\)から平均処置効果（CATE）\(τ\)を予測する機械学習モデルをMeta-learnerと呼びます。数式で書くと\(τ=M(X)\)となります。このモデルMの設計の違いにより異なるMeta-learnerが定義できます。大雑把には、処置群と対照群とで\(Y(1)\)と\(Y(0)\)を単一モデルで予測して、それらの差分を処置効果\(τ\)とするS-learner（Sはsingleを意味します）と、\(Y(1)\)と\(Y(0)\)を異なる2つのモデルで予測して、それらの差分を\(τ\)とするT-learner（Tはtwoを意味します）があります。

S-leanerもT-learnerもともに処置群と対照群の共変量分布の違いを補正することはできません。そこで改善策として、\(Y(1)\)と\(Y(0)\)の予測値を傾向スコアで補正した擬似結果の差分を改めて機械学習モデルで学習する手法が考えられます。こうした手法の代表例として DR-learner（Doubly Robust learner）やDA-learner（Domain Adaptation learner）が知られています。

DiffPOの場合、CATEは学習済みの条件付き分布\(p(Y|A,X)\)によるサンプリングによって推定されます。具体的には一定回数サンプリングを行って得られたサンプル群の平均値（または中央値）として決まります。今回の検証では、100回サンプリングを行った中央値を推定値として採用しました。

評価指標としては、CATE推定値の予測誤差（PEHEと呼びます）を採用します。DiffPOをMeta-learner4種と比較した結果は以下のグラフの通りです（図9）。棒グラフの高さとエラーバーは、10分割交差検証の平均値 と標準偏差を表しています。

グラフからDiffPOが最もPEHEが小さく予測精度が高いことが分かります。S-learnerとT-learnerはともに選択バイアスが傾向スコアにより補正されていないため、PEHEが他と比べて大きくなっています。傾向スコア補正を取り込んだDR-learnerとDA-learnerは、S-learnerやT-learnerよりはPEHEが小さく抑えられていますが、DiffPOには及びませんでした。DiffPOが最も高精度な理由として、傾向スコアを損失関数に直接取り込んでいるため、DR-learnerなどのように傾向スコア補正の定義の恣意性やモデルの2段階学習の影響を受けないからと考えられます。

最後に、DiffPOの場合、共変量に応じて潜在的結果の分布を直接可視化できることを示しておきます。図9 左は処置ありと処置なしの2つの分布が乖離していて処置効果が有意に認められるケース、図9 右は両分布の重なりが大きく処置効果が認められないケースです。分布として効果を評価できるため、実際に処置をした場合の効果の確実性や逆効果になるリスクを評価することができます。

今回の検証では、Meta-learnerとの比較しか行っていませんが、因果推論に特化した機械学習手法としてCausal-treeが知られています。Causal-treeとDiffPOとの比較は今後の検証課題です。

まとめ

本稿では、拡散モデルのデータサイエンスへの応用事例を2つ紹介しました。表形式データの生成においては、画像データと同様に、GANやVAEに比べて拡散モデルによる手法が安定で高精度であることが示されました。因果推論への応用においては、拡散モデルによる手法がMeta-learnerに比べて高精度であること、点推定値だけでなく分布も推定できるという利点が示されました。

予測値の分布を推定することは、拡散モデルに限らずベイズ推定やガとウス過程回帰などでも可能です。ただし、ベイズ推定では事前分布を設定する必要があることと、シミュレーションの計算コストに課題があります。ガウス過程回帰ではカーネル関数の選択基準や計算コストに課題があります。

その点、拡散モデルは、ニューラルネットワークで学習することが前提ですが、表形式データや治験データを扱う限り、計算コストは画像データ生成と比較してずっと低く抑えられます。さらに、任意の複雑なデータ分布を多段階のノイズ除去によって再現できるという利点もあります。

このように、拡散モデルは汎用性および再現性が高いだけでなく、拡散ノイズのスケジューリングとニューラルネット構造の設定以外に事前のモデル設定が必要ないという点で、既存手法に比べて優位性が認められます。今後、データサイエンスの現場においても、拡散モデルが活躍する機会が増えることが期待されます。

付録